CONTENIDO Mensaje del Director Liderazgo Anáhuac Humor Reto al Intelecto Checa esto

Marzo 2007 Números Anteriores

1. El Centro de Alta Dirección en Ingeniería y Tecnología (CADIT), Área de Posgrado de la Facultad de Ingeniería, será sede del Seminario Internacional para formar docentes especializados en Minería de Datos. El Sr. Jerry Oglesby, director de Higher Education and Global Consulting Certification de la División Educativa de SAS Global, visitó la Universidad Anáhuac con el objetivo de analizar la viabilidad de que el proyecto fuera encabezado por el Dr. Viterbo Berberena, coordinador del Área. En los 4 años que lleva este programa de formación es la primera vez que se designa una sede fuera de Estados Unidos, a la cual asistirán docentes de Asia, Europa, América y Oceanía.

2. El Dr. Víctor Hugo del Valle, coordinador de la carrera de Ingeniería Química para la Dirección, presentó a un grupo de preuniversitarios de los colegios Vista Hermosa, Instituto Irlandés, Colegio Alemán, Colegio Tepeyac, CENCA, Colegio Oxford, Colegio del Bosque e Instituto Cumbres, la licenciatura Ingeniería Química para la Dirección. En dicha sesión el Dr. Del Valle habló de los procesos que enseñan a convertir la materia prima en productos innovadores. Docentes de jerarquía internacional, instalaciones con la más alta tecnología y una formación de liderazgo impulsarán a los alumnos interesados en la química y sus procesos a dominar las ciencias térmicas y de fluidos, el diseño de equipos, la energía y el desarrollo sustentable.

3. El Dr. Gabriel Carmona, coordinador del Doctorado en Ingeniería Industrial del CADIT, escribió el artículo de portada de la revista Manufactura, de Editorial Expansión, "Es un pequeño lujo, pero ¿lo valgo?", mismo que analiza si los sistemas de Planeación de Recursos Empresariales (ERP) son para la empresa de manufactura un lujo o una necesidad. Además, en dicho artículo revisa su evolución, el proceso de adquisición, implementación y la operación de un ERP. El número especial correspondiente a marzo establece la importancia del ERP en la logística. Cabe señalar que el Dr. Carmona fue invitado en 2006 formar parte del Consejo Editorial.

4. La Dra. María Elena Sánchez, coordinadora del Área de Mecatrónica, dicta el curso Trabajo en equipo para lograr un aprendizaje significativo. En él, el profesor conocerá los cinco elementos básicos del aprendizaje colaborativo y los diferentes equipos de trabajo en que debe dividir a los alumnos para realizar con éxito las tareas colaborativas que abarcan desde las actividades en clase hasta proyectos semestrales. El curso, dirigido a docentes y organizado por el Centro de Formación Docente (CEFAD), incluye la enseñanza y aplicación de diferentes métodos grupales de trabajo en clase y la planeación de actividades. La Dra. Sánchez también acaba de publicar en Spectroquimica el artículo "Electrical and optical properties of C46H22N8O4KM (M=Co, Fe, Pb) molecular-material thin films prepared by the vacuum thermal evaporation technique" y "Evaluación de la movilidad del boro en aceros al carbono y herramienta en el proceso de borurización en pasta", en Revista Científica.

En este número, presentamos a nuestros amables lectores (que han ido creciendo a ritmo casi de progresión geométrica, y ¡gracias!), dos acertijos sobre colocación de números en celdillas:

1. Triángulo mágico. Coloca los números enteros naturales del uno al nueve en los lados del triángulo de la figura siguiente (un número en cada compartimiento), de tal forma que la suma en cada uno de los tres lados sea 17.

Hay varias soluciones esencialmente diferentes, es decir, que no se obtengan de otra solución previa mediante rotaciones o reflexiones del triángulo. ¿Cuántas soluciones eres capaz de hallar?.

2. Cuadrado mágico. Coloca ahora los mismos nueve dígitos en las celdillas del cuadrado siguiente, de tal suerte que sumen 15 de ocho maneras distintas: en cada una de las tres filas, las tres columnas y las dos diagonales.

En este caso, la solución sí es única, lo que quiere decir que cualesquiera dos soluciones son esencialmente iguales o isomorfas, pudiéndose obtener una a partir de otra mediante rotaciones o reflexiones de la figura.

¡Y gracias a nuestros lectores por las numerosas cartas recibidas. En breve se les dará respuesta a todas ellas!

Envía tu solución o comentarios a la dirección del Dr. Gabriel Velasco Sotomayor: gvelasco@anahuac.mx con la leyenda de asunto "respuesta al reto intelectual"

 

Una inquietud muy usual en un niño curioso (cómo lo fui yo mismo en su momento) se relacionaba con la idea de que nuestro "mundo" pareciera ser algo pequeño y localizado. Al fin y al cabo, cuando todavía no tenemos la preparación suficiente como para entender la "redondez" de la Tierra, nos da por pensar que nuestro entorno se limita exclusivamente a aquello que alcanzamos a ver. Es decir, ni siquiera se nos ocurre pensar que detrás de esa línea que llamamos horizonte todavía hay mucho más "mundo". El hecho que no lo veamos o no lo imaginemos no necesariamente significa que no existe.

Esta sensación de límite se refuerza notablemente cuando se tiene la oportunidad de visitar alguna localidad costera y ver el mar. Para las criaturas terrestres quienes viven en "tierra adentro" la primera visión del mar es algo inolvidable.

Recuerdo, en mi caso siendo todavía un niño de ocho años de edad, el enorme asombro que experimenté al momento de transponer la última cumbre justo antes de llegar por carretera a Acapulco (todavía no era la Autopista del Sol ni había túnel). A medida que bajábamos por el último tramo hacia la bahía quedé azorado ante esa imponente visión del mar como una inconmensurable y planísima extensión de color azul profundo y limitada por esa línea incondicionalmente recta que daba paso a un cielo todavía más azul y brillante por encima. Eso fue hace muchos, muchísimos, años pero cada vez que viajo a Acapulco nuevamente experimento esa maravillosa sensación.

Y, cómo aquel niño curioso que era, surgió el alud de preguntas. Así aprendí que esa línea que separa al mar del cielo se llama horizonte; que dicho horizonte no representa el final del mundo puesto que más allá sigue habiendo mar; que a medida que viajamos al horizonte éste se aleja pues, en realidad, nunca lo alcanzamos, etc. En fin, se me proporcionó mucha información útil e interesante. Pero, mis parientes, quienes hacían esfuerzos por brindarme todas las explicaciones requeridas, no pudieron con la última pregunta:

- ¿Y, a qué distancia está el horizonte?

Nadie pudo darme una respuesta concreta. Todas fueron elucubraciones y, cuando mucho, un tío quien estuvo en la Marina me dijo que la distancia aproximada era "como de doce millas náuticas" o sea algo más de veinte kilómetros.

Empero, con el paso del tiempo y el acopio de madurez, estudios e información comencé a percatarme que el horizonte se aprecia más lejano conforme nos situamos en un punto más elevado. Así, estado parado junto a la orilla del mar y con las olas mojándome los pies, el horizonte parecía algo cercano; casi se le podía tocar, por decirlo así. Luego, al subir a uno de los pisos altos en el hotel donde me alojaba observé claramente que el horizonte ya se apreciaba algo más lejano. Más tarde, salí a caminar y llegué a la cima de un cerro desde donde ya me percaté de un horizonte bastante más retirado que aquel visto desde la orilla del mar.

Varios años después, ya bastante crecidito pero no menos curioso, viajé a Acapulco por la vía aérea. Fue entonces, tras el despegue de regreso hacia la Ciudad de México y a medida que el avión tomaba altura que tuve la oportunidad de divisar un horizonte tan, pero tan lejano que ya no era una línea bien definida. Más bien, lucía borroso pero, eso sí MUY lejos. ¿Por qué?, ¿Cómo lo explico? fueron las preguntas que mantuvieron ocupada mi mente el resto del vuelo y mucho tiempo después.

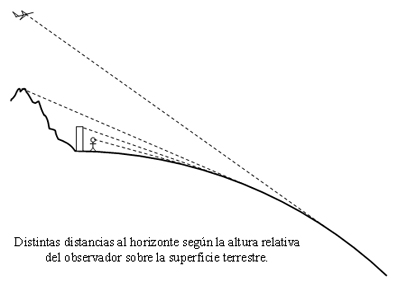Así pasaron los años. Ya contratado aquí en la Universidad Anáhuac como Coordinador de la Especialidad en Telecomunicaciones tomé la responsabilidad para preparar e impartir un curso sobre comunicaciones satelitales. Muy estrechamente relacionado con esta disciplina tecnológica se tiene el concepto referente al área de cobertura sobre la porción de la superficie terrestre que resulta visible desde un satélite ubicado en órbita a gran altitud. De hecho, ese fue uno del los principales argumentos de Arthur C. Clarke, allá por el año de 1945, cuando publicó un genial artículo proponiendo el desarrollo de estos, en aquel entonces, novedosos sistemas^[CHK-SAT].

En realidad este cuestionamiento de distancia al horizonte es un problema bastante sencillo de resolver. Todo se reduce al análisis del triángulo rectángulo que se forma si se eligen el centro de la Tierra (punto O), el observador (punto S) y el punto de tangencia (punto H) que la visual de dicho observador forma con respecto a la superficie terrestre como vértices del mencionado triángulo. Por añadidura se define el punto K que corresponde al punto "sub-observador" (directamente por debajo del observador) sobre la superficie terrestre.

Para construir la figura ilustrada en la página siguiente debe recordarse que para toda circunferencia se cumple necesariamente que una recta tangente a la misma forma un ángulo recto con el radio trazado a partir de dicho punto de tangencia. Se definen los siguientes elementos en la figura referida:

La dirección dada por la recta OKS es la llamada vertical local para el punto K de la superficie terrestre sobre el cual se ubica el observador.

En forma semejante, la dirección dada por la recta OH es la vertical local para el punto H donde la visual del observador forma tangencia con la superficie terrestre.

Por último, la dirección correspondiente a la recta SH representa la llamada horizontal local, en la dirección hacia S, tomada sobre el punto H de tangencia antes citado.

Debido a que una recta vertical y otra horizontal con un punto en común (punto H) son, por definición, perpendiculares entre sí, sigue que:

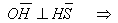El triángulo OHS es rectángulo y, por tanto, cumple el Teorema de Pitágoras.

Ahora, se definen las siguientes longitudes en esta figura:

Con base en el Teorema de Pitágoras:

Ahora bien, tal como ya se citó en una edición anterior del ¡Checa Esto!^[CHK25], se sabe que el radio terrestre equivale a 6,378.1370 kilómetros. Así, al sustituir esta cifra en la expresión matemática recién obtenida resulta factible determinar la distancia al horizonte d en función de las distintas alturas h a las cuales el observador se posicione sobre la superficie terrestre.

Por ejemplo, la estatura promedio de los Seres Humanos es de 1.70 metros. Si se considera que los ojos se encuentran aproximadamente 10 centímetros (0.10 metros) por debajo de la coronilla, tenemos que la visual (el denominado como punto S en la figura) está a una altura de 1.60 metros o, bien, a 0.00160 kilómetros sobre el nivel del suelo. Así, al aplicar los valores numéricos a la ecuación, sabremos para esa persona "promedio" parada junto a la orilla del mar el horizonte está a una distancia de 4.518 kilómetros.

Obviamente, al aumentar la altura, incrementará correspondientemente la distancia al horizonte. Surge pues, una reflexión curiosa. Si dos personas de distintas estaturas se encuentran paradas juntas -hombro con hombro- en la orilla de la playa viendo hacia el mismo punto sobre el mar, resultará que cada quien ve un horizonte distinto. Literalmente y no en sentido figurado. De aquí que una mayor estatura podría representar una cierta ventaja (aunque también tiene sus desventajas; por ejemplo, los grandulones se lastiman más al caer desde más arriba).

Y, entonces, ¿qué ocurre cuando se sube a un piso alto, a la cima de un cerro o a un avión? La tabla a continuación ofrece el detalle respectivo y, de paso, resuelve mis inquietudes de antaño.

h [metros]	h [kilómetros]	Situación	d [kilómetros]
1.60	0.0016	Parado junto a la orilla del mar	4.518
16	0.016	Desde un quinto piso	14.286
160	0.160	Desde la cima de un cerro junto a la costa	45.178
1,600	1.600	En un avión que toma altura o se aproxima	142.873
10,058	10.058	En un avión en pleno vuelo (a 33 mil pies)	358.335

No solamente se explica con toda claridad por qué el horizonte aparenta estar cada vez más lejos a medida que se sube. También se justifica la razón para que dicho horizonte se vea borroso desde un avión. Es ya tanta la distancia que la bruma y el vapor de agua, normalmente presentes en la atmósfera, se tornan factores importantes cuando se pretende divisar objetos tan lejanos.

Pero, además, surgen otras conclusiones tan sorprendentes que mejor será dejarlas para la próxima entrega de esta serie.

Continuará...

---

[CHK-SAT]: Reider, J.N. (septiembre y octubre 2006, febrero 2007); "¡Checa Esto! núms. 024, 025 y 026"; México: Universidad Anáhuac, Boletín Interno, Facultad de Ingeniería.

[CHK25]: Reider, J.N. (octubre 2006); "¡Checa Esto! núm. 025"; México: Universidad Anáhuac, boletín interno, Fac. de Ingeniería.